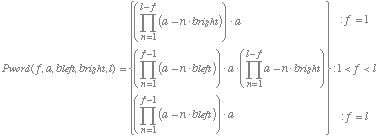
Letter legibility and visual word recognition

Letter legibility and visual word recognition

Tatjana A. Nazir

Center for Research in Cognitive Neuroscience

C.N.R.S, Marseille, France

Arthur M. Jacobs

Philipps-Universtität, Marburg, Germany

and

Center for Research in Cognitive Neuroscience

C.N.R.S, Marseille, France

J. Kevin O'Regan

Laboratoire de Psychologie Expérimentale

C.N.R.S, Paris, France

Running head: Letters and words

Mail address. Tatjana A. Nazir, Center for Research in Cognitive Neuroscience (CNRS - CRNC), 31, Chemin Joseph-Aiguier 13402 Marseille Cedex 9, France. Tel.: (33) 04.91.16.41.13. E-Mail: Nazir@lnf.cnrs-mrs.fr

Abstract

Word recognition performance varies systematically as a function of where the eyes fixate in the word. Performance is maximal with the eye slightly left of the center of the word, and decreases drastically to both sides of this 'Optimal Viewing Position'. While manipulations of lexical factors have only marginal effects on this phenomenon, previous studies have pointed to a relation between the viewing position effect and letter legibility: When letter legibility drops, the viewing position effect becomes more exaggerated. To further investigate this phenomenon, we improved letter legibility by magnifying letter size in a way that was proportional to the distance from fixation (e.g. TABLE). Contrary to what would be expected if the viewing position effect were due to limits of acuity, improving the legibility of letters has only a restricted influence on performance. In particular, for long words, a strong viewing position effect remains even when letter legibility is equalized across eccentricities. The failure to neutralize the viewing position effect is interpreted in terms of perceptual learning: since normally, because of acuity limitations, the only information available in parafoveal vision concerns low-resolution features of letters, even when magnification provides better information, readers are unable to make use of it.

The legibility of a letter is known to decrease with its distance from the position where the eye is fixating (Anstis, 1974; Bouma, 1970; Nazir, O'Regan & Jacobs, 1991; Nazir, Heller & Sussmann, 1992; Olzak & Thomas, 1986; Townsend, Taylor, and Brown, 1971). Even for unlimited presentation durations, the probability of identifying a letter in a random string drops from a value of one for the directly fixated letter to approximately 0.4 for a letter presented only five letter locations away from the center of gaze (Townsend et al., 1971). Given that during normal reading many words are fixated only once, and given that the average fixation duration is less than 250 ms (e.g., Rayner & Pollatsek, 1989), these limits of acuity must necessarily affect word recognition performance: We expect a word to be recognized best when the eye is fixating its center, where the largest number of letters benefits from high resolution.

Eye movement behavior during normal reading seems to confirm this hypothesis. The probability that a word is fixated more than once is minimal when the eye lands near the middle of a word, and increases as the eye's initial fixation position deviates either leftwards or rightwards from this "Optimal Viewing Position" (McConkie, Kerr, Reddix, Zola, & Jacobs, 1989; O'Regan, Lévy-Schoen, Pynte, & Brugaillère, 1984; Radach & Kempe, 1993; Underwood, Clews, Everatt, 1990; Vitu, O'Regan, & Mittau, 1990; Vitu, 1991a). Under the assumption that refixations result from the failure to identify the word during the previous fixation, this behavior is compatible with the hypothesis that the amount of available visual information differs significantly as a function of the eye's first location in the word. The existence of a strong viewing position effect during word recognition has also been confirmed using dependent measures other than eye movements. Naming latencies and lexical decision times (when the eye is free to move in the word) are shortest when the eye starts to fixate the word near its center (Brysbaert & d'Ydewall, 1988; O'Regan et al., 1984; O'Regan & Jacobs, 1992), and the probability of correct lexical decision and correct identification (when only one fixation is allowed in the word) is higher with the eye near the center than when the word is fixated towards the beginning or the end (e.g., Brysbaert, Vitu, & Schroyens, 1996; Farid and Grainger, 1995; Nazir, 1993; Nazir et al., 1991; 1992).

Characteristics of the viewing position effect

A typical pattern of the viewing position effect (VPE) for five to nine-letter words is shown in Figure 1 (solid symbols; data replotted from Nazir, 1993). The data were collected in a lexical decision task where participants were asked to decide whether a briefly presented letter string was a word or not. The experimental technique consisted of presenting the letter string laterally displaced in relation to a fixation point such that on its appearance, the eye was fixating one of five fixation zones in the word (each stimulus string was divided into five equally wide zones of one fifth of the width of the total word length. Thus, the zones for a 5-letter string were one-letter wide; for a 9-letter string, they were 1.8 letters wide. The center of each zone was designated as a potential initial fixation point). As can be seen from the figure, performance for all word lengths varies systematically with the location of the eye in the word. Overall performance, indicated in the right upper corner of each panel, drops on average for 3.3% with each additional letter of word length, and the VPE becomes stronger for longer words. Note however that all curves are asymmetric. The optimal viewing position is systematically left of and not at word center.

At first glance, this asymmetry contradicts the hypothesis of a direct relation between the VPE and letter legibility. Since acuity drops symmetrically to both sides of fixation (Olzak & Thomas, 1986), symmetrical curves are expected. O'Regan and Jacobs (1992) hypothesized that this shift of the optimal viewing position away from the center of the word is related to the informational and/or morphological structure of words. If the first half of words tends to be more "informative" than the second half (in the sense that only few other words share the same beginning with a given target word), there might be an advantage in fixating left of the center of a word. However, for this hypothesis to be correct, the optimal viewing position should move into the second half of words when the word stimuli are chosen to be more informative at their ends (e.g., for words like "interview", which shares its prefix with many other words). O'Regan et al. (1984; see as well Holmes and O'Regan, 1987 and Brysbaert et al., 1996) showed some empirical evidence in favor of such a dependence of the viewing position effect on the informational/morphological structure of words. However, the observed dependence was very small, and furthermore, in none of the reported experiments did the optimal viewing position shift rightwards beyond the center of the word.

Other investigators like Brysbaert and d'Ydewalle (1988), suggested that the leftward shift of the optimal viewing position is related to hemispheric differences in language processing. To test this hypothesis the authors measured word recognition as a function of viewing position for left and right hemisphere dominant participants. Although right hemisphere dominant participants performed slightly differently from left dominant participants, none of the right dominant participants ever showed an optimal viewing position in the second half of the word. Thus, as was the case for the informational structure of words, hemispheric differences in language processing do not explain the strong and robust asymmetry in the VPE.

As an alternative, Nazir et al. (1991) proposed that the observed asymmetry is caused by differences in the visibility of letters on the two sides of the fixation point. The probability of recognizing letters, especially when they are embedded in strings, is higher when the letters are presented in the right than in the left visual field (e.g., Bouma, 1973; Bouma & Legein, 1977; Hagenzieker, van der Heijden, & Hagenaar, 1990; Nazir et al., 1991). According to an estimation by Nazir et al. (1991) the ratio of this left/right asymmetry in the legibility of letter is approximately 1.8/1. Thus, when the probability to recognize a target letter drops from 1 at the center of gaze to .9 at a given eccentricity in the right visual field, it drops to .82 when the letter is presented at the same eccentricity in the left visual field. When a word has to be recognized it is therefore advantageous to fixate to the left of the center of the word so that fewer letters have to be identified in the left visual field. A simple mathematical model proposed by Nazir et al., (1991) illustrates this idea (see also McConkie et al., 1989 for a similar model predicting refixation probabilities).

A model to account for the VPE.

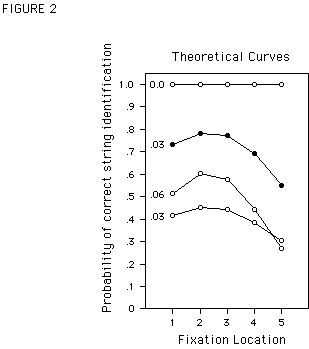
In the model by Nazir et al. (1991) it is assumed that: i) word recognition is letter-based (see Massaro and Klitzke, 1977); ii) letters of a word are recognized independently of each other; and iii) the contribution of a given letter to the recognizability of a word is proportional to its legibility. Table 1 illustrates a hypothetical example where the probability of recognizing a directly fixated letter in a string of five letters is assumed to be 1. Given the uniform drop in acuity characterized by the linear increase of the eyes' minimum angle of resolution over the central 10° of the visual field (e.g., Olzak and Thomas, 1986), we shall, for the sake of illustration, suppose that the probability of identifying neighboring letters in a string drops by a constant value, say .03, with each letter going rightwards into peripheral vision. Thus, the probabilities of recognizing the letter immediately to the right of the fixated letter will be .97, for the following letters it will be .94, .91, and so forth. Taking the aforementioned left/right asymmetry of letter legibility into account, the probability of recognizing the letter immediately to the left of fixation will drop by a value of .03 * 1.8 = .054 with each letter of eccentricity. Thus, the probabilities of recognizing the letters to the left of the fixated letter will be .946, .892, .838, and so forth. The probability of recognizing the entire string can be estimated by multiplying the probabilities of recognizing the individual letters (see last column of Table 1 and solid symbols in Figure 2)1. As can be seen from this example, the predicted probability of recognizing a five-letter string varies with fixation location in a similar way as is observed during word recognition.

Evidence for a relation between the VPE and letter legibility

Some supporting evidence for the assumed relation between the VPE and letter legibility comes from the observation that the same drop-off rate of letter legibility predicts the VPE for short and long words. For any fixation location and string length theoretical probabilities of correct word recognition can be estimated by equation:

(1)

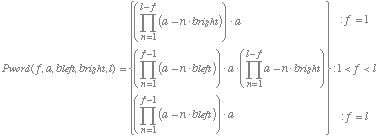
where Pword(f, a, bleft, bright, l) is the probability to recognize a word as a function of f, the relative location of the fixated letter in the string (in letter units); a, the probability to recognize the directly fixated letter; bleft and bright, the drop-off rate of the probability to recognize a letter with increasing eccentricity, going left- and rightwards, and l, the length of the word. With parameter a = 1, we estimated parameter bleft and bright from the empirical viewing position curve for 5-letter words in Figure 1. To do so, the values of bleft and bright were adjusted step by step until the shape of the theoretical viewing position curve matched the shape of the empirical curve for 5-letter words (root mean square deviation between the theoretical and the empirical curve served as a goodness of fit measure). This was the case for a bleft value of .057 and a bright value of .03. (Note that the estimated ratio of the left/right asymmetry in the legibility of letter is 1.9/1, which is very close to the ratio of 1.8/1 obtained by Nazir et al., 1991). Once fixed, the same values for the three parameters were used to calculate the theoretical curves for the remaining word lengths. The theoretical viewing position curves are presented together with the empirical curves in Figure 1 (open symbols). As can be seen from this comparison, although the height of the curves are systematically underestimated, the VPE (i.e. the shape of the curve) is captured by the model. To facilitate the comparison we shifted the theoretical curves up to the height of the empirical curves (see gray curves in Figure 1) by adding a constant h to equation (1). Table 2 gives the value of h for every word length, when root-mean square deviations (RMSD's) between the shifted theoretical curves and the empirical curves are minimal. The corresponding RMSD's are supplied in the Table (see Appendix for calculations of RMSD's). Note that our model considers only visual factors. The discrepancy in height between the theoretical and the empirical curves - indicated by h - might therefore be explained by lexical factors. Support for this hypothesis comes from the observation that the height of the word recognition curves changes with word frequency (e.g., McConkie et al., 1989; O'Regan and Jacobs, 1992; Vitu, 1991a).

However, although the strengthening of the VPE with increasing word length is captured by the model, the discrepancy between the empirical and the shifted theoretical curves becomes bigger as words become longer (see RMSD values in Table 2). This disparity is partly due to a floor effect. When string length increases the theoretical curves drop considerably and as a consequence the steepness of the branches of the curves becomes less pronounced. Thus, for a given drop-off rate the theoretically predicted VPE might be more pronounced for short than for long words. However, as we will point out later, other factors contribute to the observed misfit.

A test of the model by Nazir et al. (1991).

In the following study we will test the assumption concerning the relation between letter legibility and the VPE, by manipulating the legibility of letters in words. According to the model, manipulation of the legibility of letters in words will affect the shape of the word recognition curve in a systematic way. If instead of .03, like in Table 1, parameter bright drops by a value of .06 per letter of eccentricity, indicating that the relative legibility of letters has decreased, the height of the word recognition curve is predicted to drop marginally, and the VPE (i.e. the steepness of the branches of the curve) is significantly strengthened. With a drop-off rate of zero (this indicates that independently of their eccentricity, all letters of the word are identified equally well), the curve becomes flat. On the other hand, if the drop-off rate remains .03 but overall letter legibility - i.e., parameter a - decreases (e.g., if instead of 1 the directly fixated letter is recognized only with a probability of .9), the VPE is predicted to be almost unaffected. But now overall performance drops considerably (see Figure 2 for these different examples).

Nazir et al. (1992) showed that the VPE changes indeed in the way predicted by the model. The authors manipulated the drop-off rate of letter legibility by varying the inter-letter spaces in words. Increasing the space between successive letters increases their eccentricity, which in turn decreases their legibility. The model thus predicts a stronger viewing position effect for this case, and the prediction was confirmed by the results. As inter-letter space was progressively enlarged, the VPE became more and more pronounced. Other visual manipulations of the word stimuli that did not affect letter legibility (e.g., altering letter case) had no influence on the VPE, but a considerable effect on the height of the curve. In the present study the relative legibility of letters will be improved by magnifying the size of letters as they become further from fixation (Anstis, 1974). According to the model, the VPE should disappear when all letters of a word are perceived equally well across all eccentricities (i.e. when bleft/bright = 0; see Figure 2).

Experiment 1

Psychophysical data have shown that peripheral vision, up to approximately 10°, can be considered to be functionally an expanded version of central vision, with a magnification factor of

(1+m½) (2),

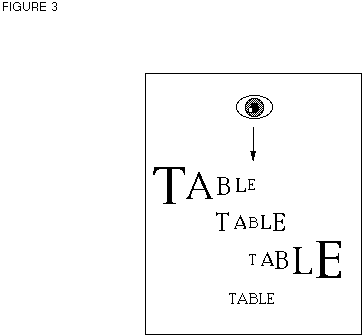
where ½ is the eccentricity in degrees and m is a magnification parameter which varies between about 0.3 and 2 depending on the type of acuity being measured (e. g., Goolkasian, 1994; Levi, Klein, & Aitsebaomo, 1985; Olzak & Thomas, 1986; O'Regan, 1989). In order to increase the relative legibility of letters, we will magnify letter size in a way proportional to their distance from fixation, following equation (2). Figure 3 gives schematic examples of the resulting word stimuli, which we will refer to as "butterfly-words". Since we do not know the exact value of m appropriate to the type of visual acuity involved in reading, we use three different m-values. According to the model, the drop-off rate of letter legibility will decrease progressively with increasing m-values, and as a consequence, the VPE for butterfly-words should progressively diminish.

Note that the drop-off rate of letter legibility is being considered here as a parameter which can vary independently of the size of the letters. This is because, although the legibility of a single letter changes with size (e.g., A vs. A), a constant size change of all letters in a word does not strongly affect the visibility of the individual letters. For example, doubling the size of all the letters of a word (e.g., TABLE vs. TABLE) makes them easier to see, but also doubles their eccentricity, and so renders them less visible again (see O'Regan, 1989; 1990). This explains why, in the model, a constant de- or increase of the size of all the letters of a word will mainly affect the height of the viewing position curve, and only to a lesser extent its shape (see the second and the fourth graph from top in Figure 2). Despite these arguments, to ensure that a flattening of the viewing position curve cannot be attributed to the fact that letters in butterfly-words are, on average, bigger than letters in words with constant-sized letters, in the work to be reported we included a control condition with constant-sized large letters. For these large words we expected a VPE comparable to the one for words with constant-sized small letters.

As in the study by Nazir (1993) participants are asked to make a lexical decision to briefly presented letter strings.

Method

Participants. Twenty-five undergraduate students from the University of Paris participated for partial course credit. All were native French speakers and had normal or corrected to normal vision.

Materials. Two hundred and fifty 5-letter and 9-letter frequent French words (average frequency ranged from 27-198 per million with a median of 57 for the 5-letter words and 28-211 per million and a median of 58 for the 9-letter words, were selected from the Trésor de la langue Française, 1971), and 250 5-letter and 9-letter pronounceable pseudowords served as stimuli. The pseudowords were constructed by replacing one or two letters in words (other than the test words) having frequencies comparable to the test words. Words and pseudowords were displayed in capital letters. The stimuli were divided into five lists; each contained 50 words and 50 pseudowords of both lengths. Stimuli of each of the five lists were presented either with constant-sized small letters, constant-sized large letters, or in one of the three 'butterfly' versions, where letter size was scaled by a factor of (1+m½), with m= 1.1, 1.3 or 1.5. At a viewing distance of 100 cm the size of the letters in the constant-sized small words subtended a matrix of .15° width and .17° height; in the constant-sized large words, they subtended a matrix of .45° width and .51° height. For the butterfly-words the directly fixated letters had the size of the letters in the constant-sized small words. The small words are therefore the reference for the butterfly-words. All stimuli were displayed in capital letters using a Times Roman vectorized font in white on dark on a Zenith video monitor, at a 50 Hz refresh rate.

Design. The experiment contained 5 blocks. In each block the stimuli of one of the five lists were presented with either constant-sized small letters, constant-sized large letters, or in one of the three "butterfly" versions. In each list each word-length category was divided into 5 groups of 10 words/pseudowords, corresponding to the five different fixation zones. The attribution of a particular fixation zone to a particular word/pseudoword group was done differently for each of five groups of participants, following a Latin Square design. Across all participants, each word/pseudoword was seen an equal number of times from each fixation zone. Another Latin Square was used to attribute one of the five lists to one of the five presentation modes. Taken over all participants, data were available for the eye fixating each of the five zones of each stimulus.

Procedure. Two vertically aligned bars appeared in the middle of the screen. Participants were instructed to fixate the gap between the bars. 500 ms after their onset, the bars were replaced by a letter string presented for 180 ms. No mask was used. The letter string was laterally displaced with respect to the fixation bars in such a way that upon its appearance, the participant's eye was positioned on one of the five letters in a 5-letter string, or on the first, third, fifth, seventh or ninth letter of a 9-letter string. The participants' task was to decide as accurately as possible whether the string was a word or not by pressing one of two keys on the computer keyboard. Participants used a chin rest.

Results and Discussion

Note that in the following we consider the results of correct lexical decisions to words only.

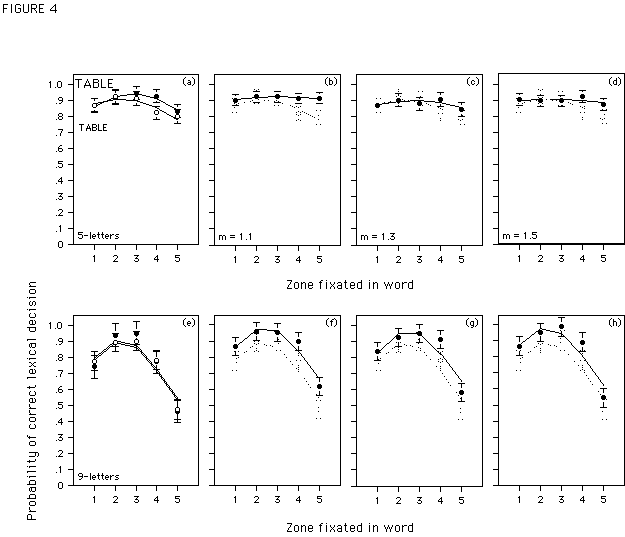
5-letter words. Figure 4 (upper panel) summarizes the results of correct lexical decisions for 5-letter words in the two control conditions (Figure 4a), and the three different magnification conditions (Figures 4bcd), together with a 95%-confidence interval around the data points (Loftus & Masson, 1994). The symbols represent empirical data, while the curves are theoretical data calculated following equation (1). For this calculation parameter a was set to a = 1. The values of parameters bleft and bright were estimated from the empirical data of the five experimental conditions. The estimated values of parameter bright, the ratio of bleft / bright, the constant h that is added to equation (1) in order to match the height of the theoretical and the empirical curve, and the corresponding RMSD's when the difference between the shifted theoretical curve and the empirical data is minimal are supplied in Table 3a. It is evident from Figure 4a that a VPE is obtained both for words with constant-sized small and constant-sized large letters. Except when fixating the fourth fixation zone, performance did not differ in the two conditions. Thus, increasing the size of all the letters of a word does not affect the VPE. On the other hand, Figures 4bcd indicate that for butterfly-words the VPE disappears (see as well corresponding values for parameter bright in Table 3a). This is already the case for the smallest m-value (m = 1.1); additional magnification (m = 1.3 and 1.5) does not further improve performance.

9-letter words. Figure 4 (lower panel) gives the corresponding results for 9-letter words, and Table 3b gives the estimates of parameter bright, and the ratio of bleft / bright. Figure 4e shows that performance for words with constant-sized small and large letters varies with the location of the eyes in the word; performance does not differ between the two conditions. Figures 4fgh and the corresponding values of bright in Table 3b show that contrary to 5-letter words, magnifying letter size as a function of eccentricity does not alter the VPE for 9-letter words. Overall performance for the butterfly-words is slightly higher than for the constant-sized small words, but the shape of the curves does not change with letter magnification. As for 5-letter words, no difference in performance is observed between the three m-values.

In short, compared to the small, non-butterfly, reference words, an equal increase in the size of all the letters in a word (constant-sized large words) has - as expected - almost no effect on performance. By contrast, magnifying letter size as a function of eccentricity (butterfly-words), affects the shape of the viewing position curve when the word is short, but its height when the word is long.

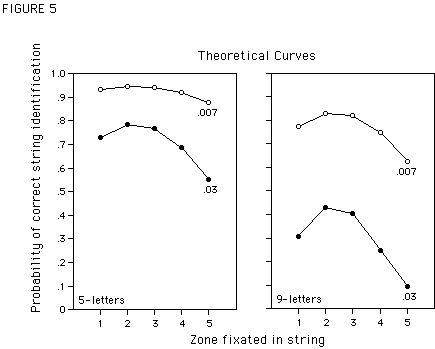
As will be shown in the following, the obtained pattern of results is indicative of an underestimation of the m-value. When m is too small to equalize letter legibility across eccentricities, magnifying letter size will be less effective for short than for long words. Suppose that in order to have equal legibility the appropriate m-value is not m=1.5, but m=1.7. To equalize the legibility of a letter presented at an eccentricity of 0.5° to a fixated letter of the size of 1°, the parafoveal letter has to be of the size of [1° * (1+1.7 * 0.5°)] = 1.85° (see equation (2)). With a magnification factor of m = 1.5 the letter size is [1° * (1+1.5 * 0.5°)] = 1.75°, which is only 1.75°/1.85°= 95% of the hypothetically necessary size. For a letter presented at an eccentricity of 3°, letter size should be [1° * (1+1.7 * 3°)] = 6.1°. However, with m = 1.5 the letter size is [1° * (1+1.5 * 3°)] = 5.5°, which is now only 5.5°/6.1°= 90% of the theoretically necessary size. In other words, if the magnification factor is underestimated, the discrepancy between the actual letter size and the size necessary to equalize legibility, increases with increasing eccentricity. As illustrated in Figure 5, our model predicts that even a small underestimation of the m-value would result in a different pattern of performance for the two word lengths. If, due to letter magnification, the drop-off rate of letter legibility decreases for example from .03 per letter position of eccentricity to .007, the predicted curve for 5-letter words is almost flat and only marginally above the reference curve. However, for 9-letter words a pronounced viewing position effect is still apparent and the main effect of magnification is on the height of the curve.

Experiment 2

To verify whether the failure to flatten the word recognition curves for 9-letter words is caused by an underestimated m-value, we designed a new experiment where the maximum m-value was increased to 1.7. In addition, we changed the smallest m-value to 0.5, and the intermediate m-value to 1.1, because the three m-values of Experiment 1 did not differ sufficiently in their effect on performance. Finally, we reduced presentation duration from 180 ms to 40 ms to prevent a ceiling effect which may have been present for the 5-letter words in Experiment 1.

In Experiment 1 we had asked our participants to make a lexical decision to the briefly presented stimuli. To generalize the results to other tasks, in Experiment 2 we additionally asked participants to name the word, once they had decided that the stimulus was a word.

Method

Participants. Twenty-five undergraduate students from the University of Paris participated for partial course credit. All were native French speakers and had normal or corrected to normal vision. None of them had participated in Experiment 1.

Materials, design and procedure. For technical reasons, in order to present 9-letter butterfly-words magnified with an m-value of 1.7, the size of the reference letter at fixation had to be decreased. At a viewing distance of 100 cm the letters in the constant-size small words (reference words) subtended a matrix of .13° width and .16° height; in the constant-size large version a letter subtended a matrix of .52° width and .64° height. The intermediate m-value was set to 1.1, and the smallest to 0.5. Presentation duration was 40 ms. As in Experiment 1 participants were asked to make a lexical decision. However, in order to minimize possible guessing effects, they were instructed to name the word once they had decided that the string was a word. The experimenter noted the answer and only trials where the word was named correctly were included in the analysis of the result. Apart from these changes, material, design and procedure were identical to the one in Experiment 1.

Results and discussion

Note that we consider only the results for correctly named words.

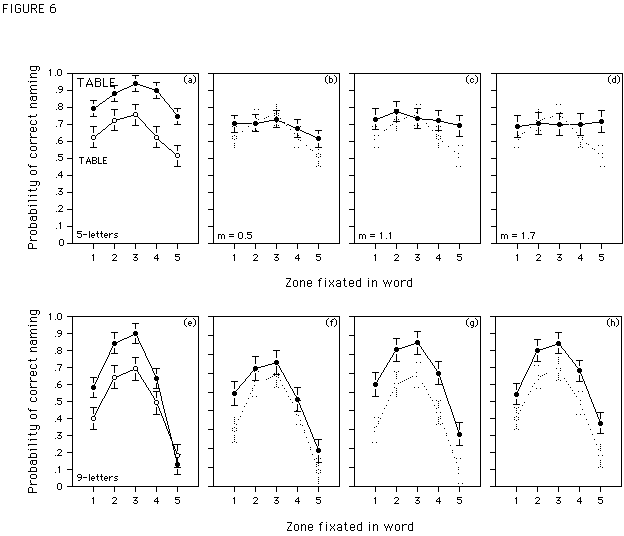
5-letter words. Figure 6 (upper panel) gives the results for correct naming of 5-letter words together with the 95%-confidence intervals. As in the previous experiment, a VPE is obtained for words with constant-sized small and large letters (see Figure 6a), though in the present results performance for large words is better than for small words. The difference in the height of these curves could be due to the absolute size of the letters in the small words. When letter size is too small and the probability to identify the letter at fixation is less than 1 (i.e., parameter a < 1), the model predicts a considerable drop of the word recognition curve, and a slightly less pronounced effect of viewing position (see Figure 2 for this prediction). Experiment 3 will confirm this hypothesis. The probability to identify the fixated letter is in fact below .75. Given this low value of parameter a estimation of bleft and bright becomes difficult, because even for small drop-off rates the predicted probabilities to recognize a word tend towards zero. For this reason we abandoned performing the estimations in this case. Thus, contrary to Figure 4, no theoretical curves are presented in Figure 6.

As in Experiment 1, magnifying letter size flattens the word recognition curves (see Figure 6bcd). With an m-value of 0.5, a weak viewing position effect is still apparent. This effect disappears, however, when the m-value is increased to 1.1. A further increase of the m-value to 1.7 has no further effect on performance. Note that the height of all word recognition curves is lower in this experiment than in Experiment 1. Since performance is highest for words with constant-sized large letters, and given that for this condition a viewing position effect still exists, the flattening of the word recognition curves for the butterfly-words cannot be attributed to a ceiling effect.

9-letter words. Figure 6 (lower panel) gives the corresponding results for 9-letter words. Figure 6e shows that performance for words with constant-sized small and large letters varies as a function of fixation location in the word. Performance for large words is better than for small words, and the VPE is slightly more pronounced in large words. As noted above, this is compatible with the assumption that the probability of identifying the directly fixated letter differs in the two conditions.

Figures 6fgh show that magnifying letter size as a function of eccentricity fails once more to flatten the viewing position curve for the long butterfly-words. As in Experiment 1, magnifying letter size had an effect on the height, but not on the shape of the viewing position curves. Compared to the small control words, overall performance increases slightly when letters are magnified with an m-value of 0.5. A further increase is observed with an m-value of 1.1, but beyond this value, increasing letter size has no further effect on performance.

Basically, Experiment 2 replicates the results obtained in Experiment 1. Magnifying letter size as a function of eccentricity affects the shape of the word recognition curves when the words are short, but it affects the height when the words are long. Note that in the present as well as in the previous experiment, letter magnification ceases to be effective after an m-value of 1.1 (this is indicated by the absence of a difference in performance for butterfly-words magnified with m-values 1.1, 1.3, and 1.5 in Experiment 1, and m-values 1.1 and 1.7 in Experiment 2). It seems thus, that the failure to flatten the word recognition curves for 9-letter words is not due to an underestimation of the m-value. Rather, we propose that it is due to an upper limit in the usefulness of the visual information made available by increasing letter size. We will come back to this point in the general discussion.

Experiment 3

To eliminate last doubts about possible contributions of visual factors in the failure to flatten the word recognition curves for 9-letter words, we designed an experiment where participants had to identify a target letter presented at various eccentricities in a string of 5 or 9 X's (e.g., XXXXXXAXX). The eye was either fixating the end or the beginning of the string, and letter size was magnified with eccentricity using the largest magnification factor of Experiment 2. If an m-value of 1.7 is still too small to equalize letter legibility across eccentricities, the probability to identify the target letter should drop with increasing distance of the target from fixation location.

Method

Participants. Ten undergraduate students from the University of Paris participated for partial course credit. All were native French speakers and had normal or corrected to normal vision.

Materials. One hundred 5-letter and 180 9-letter strings of upper-case X's served as stimuli. In each of the strings one letter was replaced by one of twenty upper-case target letters (all letters of the alphabet except the X itself and the letters I, J, L, T, Q, served as targets. I, J, L, T, Q were excluded from the set because a pilot study indicated that they were among the easiest targets to identify in the background of X's). The same target letter appeared once at each of the 5 and each of the 9 letter positions in the two strings. The strings were presented either with constant-sized letters having the same size as the letters in the small words of Experiment 2, or with letters magnified with an m-value =1.7. The same font as in Experiment 2 was used.

Procedure and design. Presentation conditions were similar to Experiment 2. However, instead of five viewing conditions, in this experiment the string appeared on the screen such that the eye was either fixating the first or the last letter in the string. Thus, half of the time the target letter had to be identified in the right, and half of the time in the left visual field. The experiment contained two blocks. In one of the blocks the stimuli were presented with constant sized small letters, in the other block the letters where magnified. 5- and 9-letter strings were presented together in one experimental block. The position of the critical letter in the string, and the presentation side of the string (right or left of fixation) was randomized. Half of the participants started with the constant-sized letter string condition, the other half with the magnified letter string condition. The task was to type the identified target letter on the computer keyboard. There was a short break half way through the experiment.

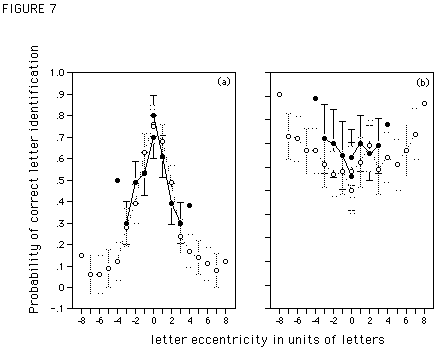
Results and Discussion

Figure 7 gives letter identification performance as a function of target eccentricity and string length, for letters presented in constant-sized letter strings (Figure 7a) and in strings with magnified letters (Figure 7b). The data are plotted along with a 95%-confidence interval, calculated separately for the two lengths and visual fields. Note, due to reduced lateral masking, the typical increase in the probability of identifying the outer letters in the string is obtained (e.g., Townsend et al., 1971; Nazir et al., 1991). These values are excluded from the calculations of the confidence intervals.

As can be seen from Figure 7a, in constant-sized letter strings target identification drops rapidly with increasing eccentricity. Note that at fixation location (eccentricity 0), the probability to identify the target is below 1. This confirms our hypothesis concerning the difference in the height of the word recognition curves for small and large constant sized words in Experiment 2.

When letter size is magnified as a function of eccentricity, target letters are recognized equally well at all eccentricities (Figure 7b). This is true for both short and long letter strings. Thus, the results of Experiment 3 further corroborate the idea that the failure to flatten 9-letter words is not due to an underestimation of the m-value.

General Discussion

Given the strong drop-off of letter legibility with eccentricity, any letter-based model of visual word recognition should predict that the probability of recognizing a word varies as a function of where the eyes fixate the word. The existence of a robust VPE during word recognition supports this assumption: A word is recognized best when the eye fixates the region around the center of a word, and performance decreases considerably when the word is fixated towards its beginning or end.

We used a simple model to allow easily testable quantitative predictions concerning the way the VPE effect should vary, if this phenomenon is related to letter legibility. Several features of the VPE could indeed be accounted for by this model. First, the fact that for all word lengths the optimal viewing position is systematically left of and not at word center is predicted by the model when the drop-off rate of letter legibility is assumed to be faster on the left of fixation than on the right (Nazir et al., 1991). Second, the strengthening of the VPE with word length emerges naturally as a consequence of the increasing number of letters that need to be processed. Third, a constant de- or increase of the size of all letters does not affect performance provided that: a) This manipulation does not change the drop-off rate of letter legibility, and b) The probability of identifying the letter at fixation is not smaller than 1. When this probability is smaller than 1, the vertical offset of the viewing position curve decreases (Experiment 2; for words with constant-sized letters). Fourth, when the drop-off rate of letter legibility is increased, the VPE becomes stronger (see Nazir et al., 1992).

All these observations indicate the existence of a relation between the VPE and letter legibility. Yet, equalizing letter legibility across eccentricities does not entirely neutralize this effect. Increasing the size of letters as they come further from fixation does improve performance in the predicted way. However, beyond an m-value of 1.1, magnifying letter size ceases to be effective and as a consequence, although the VPE disappears for short words, it remains present for long words. Both the observations that magnifying letter size has no further effects beyond an m-value of 1.1, and the fact that an m-value of 1.7 was shown to be sufficient to equalize letter legibility across all eccentricities (Experiment 3), suggest that it is not the amount of visual information available, but rather the way this information is processed that is the limiting factor here. From this point of view, improving visual conditions beyond a certain amount does not improve performance, because the information that is made available by increasing letter size may not be part of the critical information that the system has learned to use to identify words during normal reading2.

More concretely, in order to quickly identify a word during reading, the system must process efficiently all visual information available from the word during a fixation. Due to the structure of the retina, visual cues available from a letter differ as a function of where it is presented with respect to the center of gaze (e.g. Bouma, 1971; Eriksen & Schultz, 1979; Jacobs, Nazir, & Heller, 1989). The closer the letter is to the fixation point, the more details about a letter are available (i.e., high spatial frequency information). For parafoveally presented letters, mainly coarse, ambiguous features like the height-to-width quotient of the letter can be extracted (i.e., low spatial frequency information). However, although information available from a parafoveally presented letter might be ambiguous as to the identity of a letter, the combined information from all the letters in the word could be sufficient to allow correct identification of the word (Rumelhart & Siple, 1974). In fact, "ambiguous" cues from parafoveal letters can become part of the set of critical features that the system is looking for in order to quickly (though not always perfectly) recognize a word. Thus, with reading experience all visual cues available - including ambiguous features of parafoveal letters - become salient for the identity of the word. When details about parafoveal letters are made available artificially (e.g. by magnifying letter size), the infrequent use of these features in the context of a word will prevent them from being used as efficiently as the familiar "ambiguous" features. Therefore, in spite of their availability, these infrequent features, though potentially providing more information, will not contribute much to the identification of the word, and performance will remain unaffected by this manipulation.

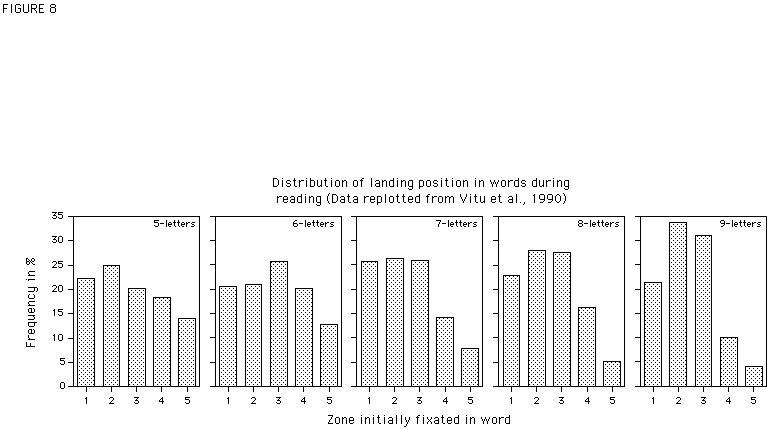
That some kind of viewing-position dependent perceptual learning takes place during reading is supported by the following observation. If we look at the landing site distribution of fixations in words during normal reading (e.g., Rayner, 1979; McConkie, Kerr, Reddix, and Zola, 1988; Vitu et al., 1990; see Figure 8 for an example), there is a striking similarity between the distribution of these initial fixations in words and the word recognition curves in Figure 1: Word recognition performance varies with fixation location in the same way as the frequency of initial fixations. This apparent "preference" of the eye to land left of the center of a word is mainly determined by visuo-motor factors, and is not a strategy adopted by experienced readers in order to optimize information extraction (e.g., McConkie et al., 1988; O'Regan, 1990; Nazir, 1991; Vitu, 1990b; Vitu, O'Regan, Inhoff, and Topolski, 1995). First-grade children locate their initial fixation on a word in much the same way adult readers do (Grimes, 1989). It seems thus that performance is best at the location where the eyes tend to land most frequently.

Note that all the arguments listed at the beginning of the General Discussion, including the compatibility between the location of the optimal viewing position and the left/right ratio of letter legibility, strongly suggest that word recognition is letter based. If a causal relation between the landing distribution and viewing position dependent word recognition performance really exists, it would therefore be misleading to interpret it as indicating that word recognition is based on some viewing position dependent global configuration of the visual stimulus. It seems rather that what is learned concerns the features of individual letters and where and how these features had been seen in the past.

References

Adams, M. J. (1979). Models of word recognition. Cognitive Psychology, 11, 133-176.

Anstis, S.M. (1974). A chart demonstrating variations in acuity with retinal position. Vision Research, 14, 589-592.

Bouma, H. (1970). Interaction effects in parafoveal letter recognition. Nature, 226, 177-178.

Bouma, H. (1971). Visual recognition of isolated lower case letters. Vision Research, 11, 459-474.

Bouma, H. (1973). Visual interference in the parafoveal recognition of initial and final letters of words. Vision Research, 13, 767-782.

Bouma, H., & Legein, Ch. P. (1977). Foveal and parafoveal recognition of letters and words by dyslexics and by average readers. Neuropsychologia, 15, 69-80.

Brysbaert, M., & d'Ydewalle, G. (1988). Callosal transmission in reading. In: G. Luer, U. Lass, & J. Shallo-Hoffmann (Eds.), Eye movement research: Physiological and Psychological aspects, (pp. 246-266). Göttingen: Hogrefe.

Brysbaert, M., Vitu, F., & Schroyens, W. (1996). The right visual field advantage and the optimal viewing position effect: On the relation between foveal and parafoveal word recognition. Neuropsychology, 10, 385-395.

Eriksen, C. W., & Schultz, D. W. (1979). Temporal factors in visual information processing: a tutorial review. In: J. Requin (Ed.), Attention & Performance, VII (pp. 3-23). Hillsdale, N. J.: Erlbaum.

Farid, M. & Grainger, J. (1996). How initial fixation position influences visual word recognition: A comparison of French and Arabic. Brain and Language, 53, 351-368.

Goolkasian, P. (1994). Size scaling and its effect on letter detection. Perception & Psychophysics, 56, 681-690.

Grimes, M. (1989). Where first grade children look in words during reading. Master's Thesis, Department of Psychology, University of Illinois at Urbana-Champaign, USA.

Hagenzieker, M. P., van der Heijden, A. H. C., & Hagenaar, R. (1990). The time courses in visual-information processing: Some empirical evidence for inhibition. Psychological Research, 52, 13-21.

Holmes, V. & O'Regan, J.K. (1987). Decomposing French words. In J. K. O'Regan & A. Lévy-Schoen (Eds.). Eye Movements: from physiology to cognition (pp. 459-466). Amsterdam: North-Holland.

Jacobs, A. M., Nazir, T. A., & Heller, O. (1989). Letter perception in peripheral vision: a temporal discrimination matrix using eye movements. Perception & Psychophysics, 46, 95-102.

Levi, D. M., Klein, S. A., & Aitsebaomo, A. P. (1985). Vernier acuity, crowding and cortical magnification. Vision Research, 25, 963-977.

Loftus, G., & Masson, M. (1994). Using confidence intervals in within-subject designs. Psychonomic Bulletin & Review, 1, 476-490.

Massaro, D. W., & Klitzke, D. (1977). Letters are functional in word identification. Memory & Cognition, 5, 292-298.

McConkie, G. W., Kerr, P. W., Reddix, M. D., & Zola, D. (1988). Eye movement control during reading: I. The location of initial eye fixations in words. Vision Research, 28, 1107-1118.

McConkie, G. W., Kerr, P. W., Reddix, M. D., Zola, D., & Jacobs, A. M. (1989). Eye movement control during reading: II. Frequency of refixating a word. Perception & Psychophysics, 46, 245-253.

Nazir, T. A. (1991). On the role of refixations in letter strings: the influence of oculomotor factors. Perception & Psychophysics, 49, 373-389.

Nazir, T. A. (1993). On the relation between the optimal and the preferred viewing position in words during reading. In: G. d'Ydewalle & J. van Rensbergen (eds.), Perception & Cognition: Advances in eye movement research, (pp. 349 - 361). Amsterdam: North-Holland.

Nazir, T. A., Heller, D, Sussmann, C. (1992). Letter visibility and word recognition: The optimal viewing position in printed words. Perception & Psychophysics, 52, 315-328.

Nazir, T. A., O'Regan, J. K., & Jacobs, A. M. (1991). On words and their letters. Bulletin of the Psychonomic Society, 29, 171-174.

Olzak, L. A., & Thomas, J. P. (1986) Seeing spatial patterns. In. K. R. Boff, L. Kaufman, & J. P. Thomas (Eds.), Handbook of Perception and Human Performance, (Vol. II., pp. 7:1-7:56). New York: Wiley.

O'Regan (1989). Visual acuity, lexical structure, and eye movements in word recognition. In B. Elsendoorn & H. Bouma (Eds.), Models of human perception (pp. 261-292). London: Academic Press.

O'Regan (1990). Eye movements and reading. In E. Kowler (Ed.), Eye movements and their role in visual and cognitive processes (pp. 395-453). Amsterdam: Elsevier.

O'Regan, J. K., & Jacobs, A. M. (1992). Optimal viewing position effect in word recognition: a challenge to current theory. Journal of Experimental Psychology: Human Perception & Performance, 18, 185-197.

O'Regan, J. K., Lévy-Schoen, A., Pynte, J., & Brugaillère, B. (1984). Convenient fixation location within isolated words of different length and structure. Journal of Experimental Psychology, Human Perception and Performance, 10, 250-257.

Radach & Kempe (1993). An individual analysis of initial fixation position in reading. In: G. d'Ydewalle & J. van Rensbergen (eds.), Perception & Cognition: Advances in eye movement research, (pp. 213-225). Amsterdam: North-Holland.

Rayner, K. (1979). Eye guidance in reading: Fixation location within words. Perception, 8, 21-30.

Rayner, K. & Pollatsek, A. (1989). The Psychology of Reading. Englewood Cliffs, NJ: Prentice-Hall, Inc.

Rumelhart, D. E., & Siple, P. (1974). The process of recognizing tachistoscopically presented words. Psychological Review, 81, 99-118.

Townsend, J. T., Taylor, S. G., & Brown, D. R. (1971). Lateral masking for letters with unlimited viewing time. Perception & Psychophysics, 10, 375-378.

Trésor de la Langue Française [French language frequency counts]. (1971). Nancy, France: Centre National de la Recherche Scientifique.

Underwood, G., Clews, S., Everatt, J. (1990). How do readers know where to look next ? Local information distribution influence eye fixations. Quarterly Journal of Experimental Psychology, 42A, 39-66.

Vitu F. (1991a). The influence of the reading rhythm on the optimal landing position effect. Perception & Psychophysics, 50, 58-75.

Vitu F. (1991b). The existence of a center of gravity effect during reading. Vision Research, 31, 1289-1313.

Vitu, F., O'Regan, J. K, & Mittau, M. (1990). Optimal landing position in reading isolated words and continuous texts. Perception & Psychophysics, 47, 583-600.

Vitu, F., O'Regan, J. K., Inhoff, A. W., Topolski, R. (1995). Mindless reading: Eye-movement characteristics are similar in scanning letter strings and reading texts. Perception & Psychophysics, 57, 352-364.

Appendix

Root-mean square deviations (RMSD's) were calculated using the equation,

(A1),

were Pi is the predicted value and Oi is the observed value, averaged over all participants.

Authors' Note

This research was supported in part by grants from the German Research

Office ("DFG-Deutsche Forschungsgemeinschaft"; Mittel der Forschergruppe

"Dynamik und hierarchisch-parallele Strukturierung von Repräsentationen

in Nervensystemen" an der Philipps-Universität Marburg) to Tatjana A.

Nazir and Arthur M. Jacobs. The authors would like to thank P. Marshal for software assistance. We are grateful to W. Estes, G. Loftus, D. Massaro, M. Montant, H. C. Nürk, and an anonymous reviewer for helpful comments concerning this work. Correspondence concerning this article should be addressed to Tatjana A. Nazir, Center for Research in Cognitive Neuroscience (CNRS - CRNC), 31, Chemin Joseph-Aiguier 13402 Marseille Cedex 9, France. Tel.: (33) 04. 91.16.41.13. E-Mail: Nazir@lnf.cnrs-mrs.fr

Footnotes

1. Adams (1979) showed that the probabilities of recognizing letters in words are not independent, in the sense that letter clusters can be recognized together. It is partly due to this dependency (orthographic structure) that we can recognize words without having seen all letters. In the frame of our model, orthographic structure could be implemented as the following. Instead of a linear drop of letter recognition probabilities with eccentricity, recognition probabilities could drop, for example, in the following way: 1, .97, .94, .94, .88, when fixated at the first letter; .946, 1, .97, .97, .91, when fixated at the second; .892, .946, 1, 1, .94, the third; .838, .892, 1, 1, .97, the fourth; .784, .838, .946, .946, 1, and fifth letter. With this letter cluster the theoretical probabilities of recognizing the whole string from the five viewing positions would be .75, .81, .79, .73, .59 (instead of .73, .78, .77, .69, .55, as in the last column of Table 1). As can be seen from these calculations, unless the letter cluster is very large, orthographic structure does not appreciably change the viewing position effect itself. For mathematical tractability we will work with the independence assumption.

2. We think that the failure to flatten the word recognition curves for 9-letter words cannot be attributed to lexical factors. Any viewing position dependent variation of word recognition performance that is related to lexical factors must be mediated by the legibility of letters. Lexical characteristics of a word do not change with fixation location. What changes is the availability of information as a function of where the eye fixates with respect to the lexically informative part of the word. By equalizing letter legibility across eccentricities, disadvantages due to non-optimal fixation locations are compensated, and therefore the viewing position effect should disappear.

Table 1

Theoretical probability of recognizing a 5-letter string as a function of fixation location.

Recognition Probabilities of Individual Letters

of a 5-Letter String

Letter position fixated in the string	Position of letter in the string					Probability of recognizing the entire string
	1	2	3	4	5
1	1	.97	.94	.91	.88	.73
2	.946	1	.97	.94	.91	.78
3	.892	.946	1	.97	.94	.77
4	.838	.892	.946	1	.97	.69
5	.784	.838	.892	.946	1	.55

Note assumptions: The probability of recognizing the directly fixated letter is equal to 1. This probability drops linearly by .03 (arbitrary value) with each letter position of eccentricity to the right of fixation, and by (1.8 x .03 = .054) with each letter position of eccentricity to the left of fixation. See text for details.

Table 2

Value of the constant h and root-mean square deviations (RMSD's) between the empirical data and the shifted theoretical data shown in Figure 1.

	h	RMSD
5-letters	.13	.013
6-letters	.19	.027
7-letters	.28	.030
8-letters	.33	.069
9-letters	.39	.048

Table 3a

Estimated values of parameter bright of equation (1), the ratio of the left/right asymmetry in letter legibility (bleft /bright), the constant h, and root-mean square deviations (RMSD's) between the shifted theoretical curves and the empirical curves of 5-letter words with constant-sized small and large letters, and the three butterfly words.

	bright	bleft /bright	h	RMSD
Small	.014	1.8/1	.01	.020
m= 1.1	.003	0.9/1	- .06	.006
m= 1.3	.009	1.2/1	- .04	.015
m= 1.5	.003	1.6/1	- .07	.014
Large	.025	1.1/1	.09	.008

Table 3b

Estimated values of the parameter, bright of equation (1), the ratio of left/right asymmetry in letter legibility (bleft /bright), the constant h, and root-mean square deviations (RMSD's) between the shifted theoretical curves and the empirical curves of 9-letter words with constant-sized small and large letters, and the three butterfly words.

	bright	bleft /bright	h	RMSD
Small	.020	1.8/1	.31	.046
m= 1.1	.018	1.7/1	.36	.036
m= 1.3	.019	1.6/1	.35	.055
m= 1.5	.018	1.9/1	.37	.060
Large	.021	1.9/1	.35	.064

Figure Captions

Figure 1. Probability of correct lexical decision for 5- to 9-letter words as a function of the zone fixated in the word (solid symbols; Data replotted from Nazir, 1993), plotted with a 95%-confidence interval (Loftus & Masson, 1994). The curves with open symbols represents theoretical data (see text). The gray curves represent the same theoretical data shifted in height to match the empirical data. The values in the upper right corner indicate observed performance averaged over all fixation zones.

Figure 2. Theoretical probability of recognizing a 5-letter string as a function of fixation location for 4 hypothetical legibility conditions. For the first three curves from top, the probability of recognizing the letter at fixation point is 1. As indicated in the panel, the drop-off rate of letter legibility with each letter of eccentricity to the right is 0 in the first, .03 in the second, and .06 in the third curve. For all curves the drop off rate to the left is 1.8 times the drop-off rate to the right. In the bottom curve the probability of recognizing the letter at the fixation point is .9, and the drop-off rate to the right is .03. The second curve from top (solid symbols) represents the values calculated in the last column of Table 1.

Figure 3. Schematic illustration of the butterfly-words when fixated either at the end, the middle or the beginning of the word, and the constant-sized small control word.

Figure 4. Probability of correct lexical decision for 5- and 9-letter words (Figure 4a-d, and 4e-h, respectively) as a function of fixation location in the different conditions of Experiment 1. Note that the symbols represent empirical data, plotted with a 95%-confidence interval, while the curves are theoretical data calculated following equation (1) and shifted for a constant value h (see text). Figures 4a and 4e represent performance for control words with constant sized small (open symbols) and large letters (solid symbols). The remaining graphs show performance for butterfly-words (solid symbols), magnified either with m = 1.1; m = 1.3; or m = 1.5. To make comparison easier, performance for the small control words (open gray symbols) is plotted together with performance for the butterfly-words.

Figure 5. Theoretical probability of recognizing 5- and 9-letter strings as a function of fixation location, for two different drop-off rates of letter legibility, calculated following equation (1). For all curves the probability of recognizing the letter at fixation is a = 1. For the lower curves (solid symbols) the drop-off rate of letter legibility bright = .03 , for the upper curves (open symbols) bright = .007. In both conditions bleft = 1.8 *bright .

Figure 6. Probability of correct naming of 5- and 9-letter words (Figure 6a-d, and 6e-h, respectively) as a function of fixation location in the different conditions of Experiment 2. Data are plotted with a 95%-confidence interval. No theoretical curves are presented in the figure. Figures 6a and 6e represent performance for control words with constant sized small (open symbols) and large letters (solid symbols). The remaining graphs show performance for the butterfly-words (solid symbols), magnified either with m = 0.5; m = 1.1; or m = 1.7. To make the comparison easier, performance for the small control words (open gray symbols) are plotted together with performance for the butterfly-words.

Figure 7. Probability of correct letter identification as a function of the distance of the target from fixation (in units of letters) when the target is presented in 5- and 9-letter strings of X's (solid and open symbols, respectively). Zero on the x-axis indicates fixation location, negative values indicate performance in the left visual field, positive values indicate performance in the right visual field. The data are plotted with a 95%-confidence interval. Figure 7a shows performance for constant-sized small letters, Figure 7b performance for magnified letters [m = 1.7].

Figure 8. Frequency of initial landing position of the eye during reading, in words of 5- to 9-letter. (Data replotted from Vitu et al., 1990).